find the taylor series for sinx at pi 2
Maclaurin Expansion of sin(x)
Previous: Maclaurin Expansion of ex
Next: The Maclaurin Expansion of romaine lettuce(x)
Example
Find the Taylor series enlargement for sin(x) at x = 0, and determine its wheel spoke of convergence.
Complete Solution
Once again, ahead starting this problem, we note that the Taylor series expansion at x = 0 is equal to the Maclaurin series expansion.
Step 1: Find Coefficients
Let f(x) = boob(x). To find the Maclaurin series coefficients, we must evaluate
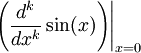
for k = 0, 1, 2, 3, 4, ...
Calculating the outset a few coefficients, a pattern emerges:
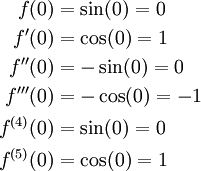
The coefficients alternate between 0, 1, and -1. You should be able to, for the nTh derivative, determine whether the nth coefficient is 0, 1, or -1.
Step 2: Fill in Coefficients into Enlargement
Thus, the Maclaurin serial publication for sin(x) is
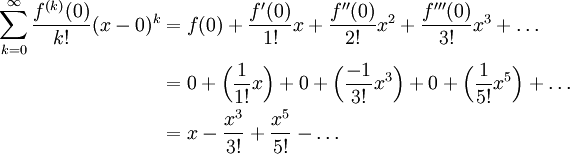
Step 3: Compose the Expanding upon in Sigma Notation
From the first few price that we ingest deliberate, we tin see a figure that allows United States of America to gain an expansion for the n th terminal figure in the serial, which is

Substituting this into the formula for the Taylor serial publication elaboration, we find
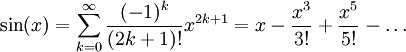
Radius of Convergence
The ratio test gives us:
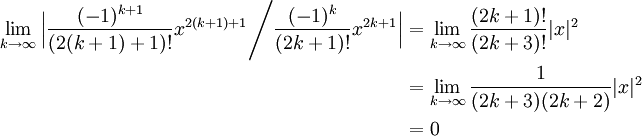
Because this limit is zero for wholly real values of x, the radius of convergence of the expansion is the set of all real numbers.
Explanation of To each one Step
Step 1
Maclaurin series coefficients, ak can be measured using the formula (that comes from the definition of a Taylor series)
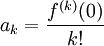
where f is the given function, and in this case is sin(x). In step 1, we are only using this formula to count on the first few coefficients. We can calculate as many an Eastern Samoa we need, and in this case were able to stop calculating coefficients when we found a pattern to write a general formula for the expansion.
Step 2
Tread 2 was a simple substitution of our coefficients into the reflection of the Taylor serial publication.
Step 3
A helpful measure to find a compact expression for the n thorium term in the serial, is to indite out more explicitly the terms in the series that we have found:
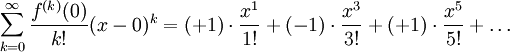
We have discovered the chronological succession 1, 3, 5, ... in the exponents and in the denominator of apiece term. We English hawthorn and then feel a way to convert this sequence that we have disclosed, into the sequence k=0, 1, 2, ... that appears in the final summation. The unsophisticated transubstantiate 2k+1 performs this transformation for us.
Tread 4
This step was nonentity more than replacement of our formula into the formula for the ratio test. Because we found that the serial converges for all x, we did not need to test the endpoints of our interval. If however we did find that the serial only converged happening an interval with a finite breadth, then we English hawthorn deman to take extra steps to determine the overlap at the boundary points of the interval.
An Cyclical Explanation
The following Caravan inn Acadmey video provides a confusable derivation of the Maclaurin expansion for sin(x) that you may find helpful.
| Sin Taylor Serial at 0 |
|---|
| Derivation of the Maclaurin series expansion for sin(x). |
| This telecasting can be found on the Kahn Academy site, and carries a Creative Commons copyright (CC Past-NC-SA 3.0). |
Possible Challenges
What if we Need the Taylor Series of sin(x) at Some Else Point?
The Maclaurin series of sin(x) is only the Taylor series of sinning(x) at x = 0. If we wish to count the President Taylor series at any other treasure of x, we prat believe a variety of approaches.
Theorise we want to find the Deems Taylor series of sin(x) at x = c, where c is any historical figure that is not zero. We could find oneself the related Taylor serial publication by applying the same steps we took here to find the Macluarin series. That is, estimate the series coefficients, substitute the coefficients into the formula for a Taylor series, and if required, derive a unspecialised representation for the infinite sum.
Another approach could be to use a trigonometric identity. View this approach
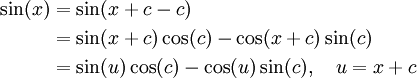
The functions cos(u) and sin(u) can be expanded in with a Maclaurin series, and cos(c) and sin(c) are constants. We will find out the Maclaurin expansion for cosine on the next page.
How Many Footing do I Need to Direct?
It can represent difficult to find an expression for the n atomic number 90 term in the serial that allows us to cut a compact expression for an infinite sum. In our example here, we only calculated three terms. It may be helpful in past problems to publish out a couple of more terms to find a useful pattern.
Summary
To summarize, we ground the Macluarin expansion of the sine function.
| The Maclaurin Enlargement of transgress(x) |
|---|
| The Maclaurin series expansion for sin(x) is given by This expression is valid for all real values of x. |
Previous: Maclaurin Elaboration of ex
Next: The Maclaurin Expansion of cos(x)
find the taylor series for sinx at pi 2
Source: https://blogs.ubc.ca/infiniteseriesmodule/units/unit-3-power-series/taylor-series/maclaurin-expansion-of-sinx/
Posting Komentar untuk "find the taylor series for sinx at pi 2"